Carlo Frabetti
El más famoso de los teoremas se demostró en el siglo sexto antes de Cristo, pero ya se conocía al menos 2.000 años antes.
Busto de Pitágoras en los Museos Capitolinos.
Mucho antes de que Pitágoras (o alguno de sus discípulos) demostrara su famoso teorema, los babilonios, los indios y los egipcios conocían -y utilizaban eficazmente- las propiedades del triángulo de lados 3, 4 y 5, que se consideraba sagrado. Lo más notable de este triángulo es que el ángulo opuesto al lado mayor es recto, y no hace falta señalar la importancia del ángulo recto en todo tipo de mediciones y construcciones. En el antiguo Egipto, el triángulo de proporciones 3-4-5 más utilizado en arquitectura y agrimensura era el de lados iguales a 15, 20 y 25 codos respectivamente (unos 7.5, 10 y 12.5 metros), llamado “triángulo isíaco” en honor a la diosa Isis, que ya se utilizó en la construcción de la pirámide de Kefrén, en el siglo XXVI a. C. Pero fueron los pitagóricos quienes, dos mil años después, demostraron el teorema y le dieron su conocida expresión canónica:
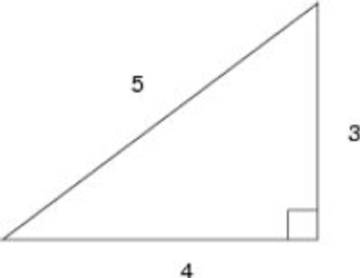
“En todo triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa”.
El ángulo recto es un elemento fundamental de nuestro entorno físico, hasta el punto de que el gran arquitecto Le Corbusier lo denominó “nuestro pacto de solidaridad con la naturaleza” y le dedicó un extenso -e intenso- poema; he aquí un fragmento:
Erguido sobre el plano terrestre / de las cosas comprensibles, / contraes con la naturaleza un pacto / de solidaridad: es el ángulo recto. / De pie vertical ante la mar, / hete ahí sobre tus piernas
Desde el momento en que se irguieron sobre sus patas traseras, los primeros homínidos debieron cobrar plena conciencia del binomio horizontal-vertical, o lo que es lo mismo, de la perpendicularidad.
Es probable que las primeras demostraciones del teorema de Pitágoras fueran geométricas, ya que los pitagóricos lo veían como una relación de los cuadrados construidos sobre los tres lados del triángulo rectángulo más que como una ecuación algebraica. Una de las demostraciones más elegantes es la que ilustra la figura (que también se encuentra representada en algunos documentos chinos muy antiguos).
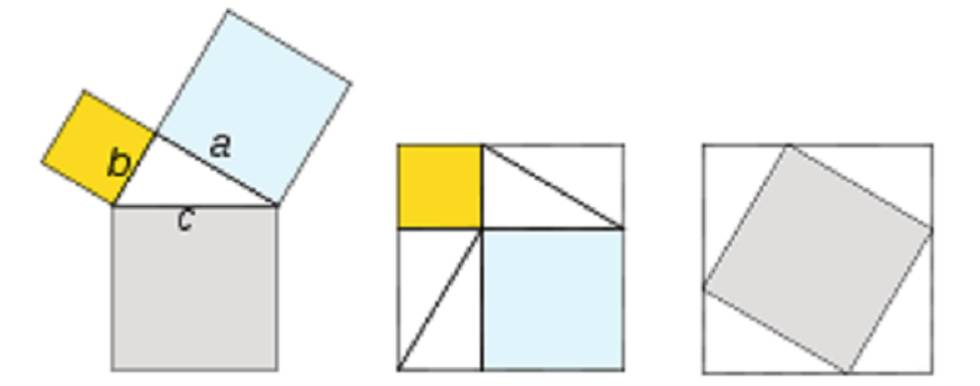
El cuadrado del centro y el de la derecha son iguales. El de la derecha está formado por el cuadrado de lado igual a la hipotenusa y cuatro triángulos iguales al original; el del centro, por dos cuadrados de lados iguales, respectivamente, a ambos catetos y cuatro triángulos iguales al original; por lo tanto, el área del cuadrado mayor es igual a la suma de las áreas de los dos menores, o lo que es lo mismo, a2 + b2 = c2.
La demostración que encontramos con frecuencia en los libros de geometría actuales (atribuida al propio Pitágoras) se basa en la semejanza de triángulos.
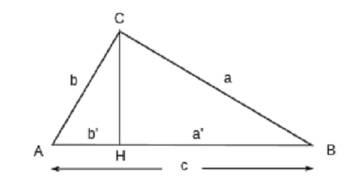
Los triángulos ABC y ACH son semejantes porque ambos son rectángulos y tienen en común el ángulo A, y por tanto sus lados son proporcionales, luego b’/b = b/c, de donde b2 = cb’. También son semejantes ABC y BCH, pues tienen en común el ángulo B, luego a’/a = a/c, de donde a2 = ca’. Sumando ambas igualdades: a2 + b2 = ca’ + cb’ = c(a’ + b’) = c2.
De Pitágoras a Fermat
La fórmula pitagórica a2 + b2 = c2 invita a preguntarse qué pasa si la generalizamos a otros exponentes y la convertimos en an + bn = cn, donde n es un número entero cualquiera. Pues bien, en 1637 Pierre de Fermat llegó a la conclusión de que para n mayor que 2 no existen tres números naturales (enteros y positivos) a, b, c tales que se cumpla esa igualdad. Fermat escribió en el margen de un libro que había encontrado una demostración “admirable” de dicho teorema; pero nunca se encontró tal demostración, y los expertos dan por supuesto que Fermat se equivocó… o quiso gastarle una broma a la comunidad matemática. De hecho, el teorema permaneció en estado de conjetura durante tres siglos y medio, hasta que, tras numerosos intentos, fue demostrado por Andrew Wiles en 1995.
“He encontrado una demostración realmente admirable, pero no cabe en el exiguo margen de este libro”, escribió Fermat. También en esto el tiempo le dio la razón: la demostración de Wiles sería difícil de encajar en los márgenes de un libro, pues ocupa unas 100 páginas.
Fórmulas Magistrales es un sección de Carlo Frabetti dedicada a explicar las principales fórmulas de las matemáticas y la física, su origen, evolución y significado preciso.
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.

No hay comentarios:
Publicar un comentario